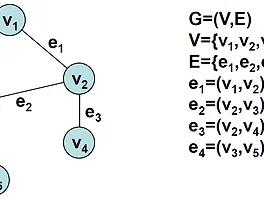
그래프의 탐색

목적 : 시작점으로부터 시작해서 모든 정점 한번씩 탐색
DFS(Depth First Search) 깊이우선탐색 - 스택(Stack) 통해 갈 수 있을 때 까지 계속 가다가 갈 수 없으면 이전 정점으로 돌아오기
1) 인접 행렬 통한 구현
2) 인접 리스트 통한 구현
3) 시간복잡도 인접행렬 O(V^2) 인접리스트 O(V+E)
BFS(Breath First Search) 너비우선탐색 - 큐(Queue) 통해 현재 갈 수 있는 정점 다 담아둔 다음에 차례로 탐색.
1) 인접 행렬 통한 구현
2) 인접 리스트 통한 구현
3) 시간복잡도 인접행렬 O(V^2) 인접리스트(V+E)
1. DFS & BFS
#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
using namespace std;
vector<bool> check;
int graph[1001][1001];
int n, m, v;
void dfs(int);
void bfs(int);
int main() {
cin >> n >> m >> v;
// 그래프 할당
check.assign(n+1, false);
for (int i = 0; i < m; i++) {
int a, b;
cin >> a >> b;
graph[a][b] = 1;
graph[b][a] = 1;
}
// dfs, bfs
dfs(v);
cout << "\n";
check.assign(n+1, false);
bfs(v);
return 0;
}
void dfs(int idx) {
check[idx] = true;
cout << idx << " ";
for (int i = 1; i <= n; i++) {
if (check[i] == false && graph[idx][i] == 1)
dfs(i);
}
}
void bfs(int idx) {
queue<int> q;
q.push(idx);
int now;
check[idx] = true;
// 비지 않을 동안
while (!q.empty()) {
now = q.front(); // 맨 앞 원소
cout << now << " "; // 출력
q.pop(); // 앞에 원소 빼기
for (int i = 1; i <= n; i++) {
// 안갔다면
if (check[i] == false && graph[now][i] == 1) {
q.push(i);
check[i] = true;
}
}
}
}
연결 요소 찾기(Connected Component)
모든 정점으로부터 DFS, BFS 탐색을 하면서 방문하지 않은 곳 처리하면 모든 연결요소를 찾을 수 있다.
2. 연결요소의 개수
문제 : https://www.acmicpc.net/problem/11724
11724번: 연결 요소의 개수
첫째 줄에 정점의 개수 N과 간선의 개수 M이 주어진다. (1 ≤ N ≤ 1,000, 0 ≤ M ≤ N×(N-1)/2) 둘째 줄부터 M개의 줄에 간선의 양 끝점 u와 v가 주어진다. (1 ≤ u, v ≤ N, u ≠ v) 같은 간선은 한 번만 주어진다.
www.acmicpc.net
풀이
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
vector<vector<int>> graph;
vector<bool> check;
int n, m, cnt, ans;
void dfs(int);
int main() {
cin >> n >> m;
graph.assign(n + 1, vector<int>(0, 0));
check.assign(n + 1, false);
// graph 입력받기
for (int i = 0; i < m; i++) {
int a, b;
cin >> a >> b;
graph[a].push_back(b);
graph[b].push_back(a);
}
// dfs 체크하기
for (int i = 1; i <= n; i++) {
cnt = 0;
dfs(i);
if (cnt == 1)
ans += 1;
}
cout << ans;
}
void dfs(int idx) {
// 갈 수 없으면 종료
if (check[idx])
return;
check[idx] = true;
cnt = 1;
for (int i = 0; i < graph[idx].size(); i++) {
int j = graph[idx][i];
if (check[j] == false)
dfs(j);
}
}이분 그래프(Bipartite Graph)
하나의 정점으로부터 DFS 탐색을 하면서 차례로 다른 영역의 그래프로 번갈아가면서 탐색이 가능하면 이분 그래프이다(다음 갈 곳이 현재 색깔과 다르면 이분 그래프가 아님).
'Archived(CSE Programming) > 알고리즘(C++)' 카테고리의 다른 글
| 다이나믹 프로그래밍(Dynamic Programming) (0) | 2019.08.22 |
|---|---|
| 그래프의 심화 (0) | 2019.08.16 |
| 그래프(Graph) (0) | 2019.08.14 |
| 브루트포스-N과 M (0) | 2019.08.14 |
| 비트마스크(BitMask) (0) | 2019.08.12 |