소수(Prime)는 소수(素數, 발음: [소쑤], 문화어: 씨수, 영어: prime number)는 자신보다 작은 두 개의 자연수를 곱하여 만들 수 없는 1보다 큰 자연수이다. 예를 들어, 5는 1x5 또는 5x1로 수를 곱한 결과를 적는 유일한 방법이 그 수 자신을 포함하기 때문에 5는 소수이다. 그러나 6은 자신보다 작은 두 숫자(2×3)의 곱이므로 소수가 아닌데, 이렇듯 1보다 큰 자연수 중 소수가 아닌 것은 합성수라고 한다. 1과 그 수 자신 이외의 자연수로는 나눌 수 없는 자연수로 정의하기도 한다.
합성수 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 합성수(合成數, Composite Number)는 1과 자기 자신이 아닌 다른 자연수의 곱으로 나타낼 수 있는 자연수를 의미한다. 1보다 큰 모든 정수는 소수이거나 합성수이다. 다음의 수는 합성수의 예이다. 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20 3333337 = 7 × 31 × 15361 2 × 3 × 5 × 7 × 11 × 13 + 1 = 30031 = 59 × 509
어려운 정의지만 간략히 정의하면 자기 자신과 1외에는 약수를 가지지 않는 수를 말한다.
이러한 소수를 구하는 방법은 말 그대로, 1부터 약수를 하나씩 체크해서 자기 자신까지 다른 약수가 있는지 체크하면 된다. 즉, 나누어 떨어지는지, 나머지가 0인지를 체크하면 된다.
그렇지만 보다 간략히 구하는 방법이 있는데, 제곱근까지 확인해도 소수인지를 체크하면 된다.
제곱근까지만 구해도 되는 이유는 간단하다. A = a*b 라고 가정했을 경우, a와 b 모두 제곱근A보다 클 수 없다. 따라서 a와 b의 곱으로 이루어진 A는 제곱근 A까지만 확인해도 소수인지 확인할 수 있다.
코드로 표현하면 다음과 같다.
// 소수 체크
bool is_prime(int a) {
// a 가 2 이하면 소수가 아니다
if (a < 2)
return false;
// a 가 2 이상이면
else {
// 2부터 제곱근까지 확인하기
for (int k = 2; k*k <= a; k++) {
if (a%k == 0)
return false;
}
// 소수
return true;
}
}
특정범위의 이러한 소수들을 구한다면, 일일이 구하면 비효율적이다. 이렇게 특정범위의 소수들을 구하는 방법 중 쉬운 방법이 하나 있는데, 그것은 에라토스테네스의 체이다.
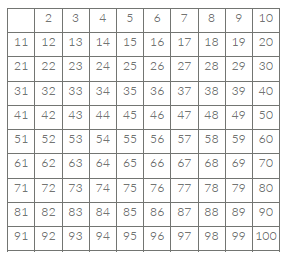
이러한 범위의 수가 있다면 경우, 2가 소수일 경우 2의 배수를 다 지운다.
그리고 3이 소수일 경우 3의 배수를 다 지운다.
이런식으로, 특정 수가 범위의 제곱근이 될때까지 반복한다.(100의 경우 11까지)

이런식으로 계속 지워나가면 완성이다.
코드로 표현하면 다음과 같다.
bool check[MAXA];
void prime_make() {
// 0과 1은 소수가 아님
check[0] = check[1] = true;
// false면 배수들 처리
for (int i = 2; i*i <= MAXA; i++) {
// 소수들의 배수는 소수가 아님
if (check[i] == false) {
for (int j = i*i; j <= MAXA; j += i)
check[j] = true;
}
}'Archived(CSE Programming) > 알고리즘(C++)' 카테고리의 다른 글
| 비트마스크(BitMask) (0) | 2019.08.12 |
|---|---|
| 재귀함수(Recursive Function) (0) | 2019.08.12 |
| 순열(Permutation) 구하기 (0) | 2019.08.07 |
| 브루트 포스(Brute Force) (0) | 2019.08.06 |
| 최대공약수(GCD) & 최소공배수(LCM) 구하기 (0) | 2019.08.05 |

