최대공약수와 최소공배수는 수학의 기본적인 내용이다.
최대공약수는 말 뜻 그대로, 두 수의 공통적인 약수 중 최대로 큰 약수이다.
최소공배수 또한, 두 수의 공톡적인 배수는 최소로 작은 배수이다.
이러한 최대공약수와 최소공배수를 구하는 방식에 대해 살펴보자.
1. 최대공약수
먼저 최대공약수의 경우, 일일이 약수를 구해서 공통되는 약수 중 가장 큰 약수를 찾는 법이 있지만,
보다 효율적으로 유클리드 호제법을 사용하면 된다.
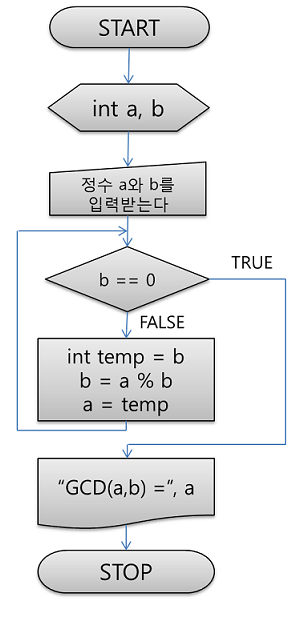
다음의 과정을 거치면 되는데, 이를 코드로 표현하면 다음과 같다.
// 최대공약수
int gcd(int a, int b) {
if (b == 0)
return a;
else {
gcd(b, a%b);
}
}생각보다 간단하다.
2. 최소공배수
최소공배수 또한 어렵지 않다.
최대공약수를 구해서 이를 최대공약수 * (A/최대공약수) * (B/최대공약수) 를 구하면 된다.
코드로 표현하면 다음과 같다.
// 최소공배수
int lcm(int a, int b) {
int gcd_ab = gcd(a, b); // 최대공약수 구해서
return gcd_ab*(a / gcd_ab)*(b / gcd_ab);
}
'Archived(CSE Programming) > 알고리즘(C++)' 카테고리의 다른 글
| 비트마스크(BitMask) (0) | 2019.08.12 |
|---|---|
| 재귀함수(Recursive Function) (0) | 2019.08.12 |
| 순열(Permutation) 구하기 (0) | 2019.08.07 |
| 브루트 포스(Brute Force) (0) | 2019.08.06 |
| 에라토스테네스의 체(소수 구하기) (0) | 2019.08.06 |

