https://programmers.co.kr/learn/courses/30/lessons/12899
코딩테스트 연습 - 124 나라의 숫자
programmers.co.kr
풀이
10 진수 | 124 진수 | 10 진수 | 124 진수 |
1 | 1 | 12 | 44 |
2 | 2 | 13 | 111 |
3 | 4 | 14 | 112 |
4 | 11 | 15 | 114 |
5 | 12 | 16 | 121 |
6 | 14 | 17 | 122 |
7 | 21 | 18 | 124 |
8 | 22 | 19 | 141 |
9 | 24 | 20 | 142 |
10 | 41 | 21 | 144 |
11 | 42 | 22 | 211 |
쉬운 듯 어려운 듯, 너무 어렵게 풀어서 결국 쉬운 풀이를 찾아봤다.
풀이의 핵심은 3진법을 생각하는데 조금 차이를 이해하는 것이다.
기본적인 3진법: 0, 1, 2, 10, 11, 12 , 20, 21, 22
124의 나라 3진법: 1, 2, 4, 11, 12, 14, 21, 22, 24, 41, 42, 44
차이점이 보인다. 바로 자리숫자에 사용할 수 있는 숫자가 한 개 더 있냐 없냐의 차이다.
일반적으로 우리는 진법을 계산할 때, 아래와 같이 나머지 연산을 통해서 거꾸로 출력하는 법을 사용한다.
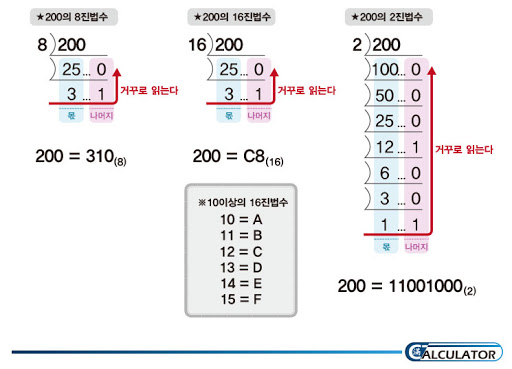
여기서도 마찬가지다. 3으로 나눈 나머지에 따라 4, 1, 2의 값을 넣어주면 된다.
1 표현 : 1 % 3 = 1
2 표현 : 2 % 3 = 2
3 표현 : 3 % 3 = 0 -> 4
단, 여기서는 앞서 말했듯이, 자리수가 하나 더 사용된다.
그 규칙을 자세히 들여다보면,
3 표현 : 3 % 3 = 0 -> 4
6 표현 : 6 % 3 = 0 -> 4 , 2 % 3 -> 2
-> 24가 되야 하는데 정답은 14이다.
9 표현: 9 % 3 = 0 -> 4 , 3 % 3 -> 0->4
-> 44가 되야 하는데 정답은 24이다.
이 값의 차이는 1, 2, 4 모두 일의 자리외에 모든 숫자에 올 수 있기 때문이다.
즉, 자리수 계산을 조금 다시 생각해볼 필요가 있다.
3으로 나누어 떨어지는 수가 올 경우 다음 값에 빼기 1을 해줘야 한다(이 논리를 이해하는데 시간이 조금 걸렸다).
기존 3진법처럼 3의 배수일 경우, 자리수가 증가하는게 아니기 때문이다.
이 공식을 통해 풀면 코드는 다음과 같다.
class Solution {
public String solution(int n) {
// 1자리 -> 1~3, 2자리 -> 4~12, 3자리 13 ~ 39
// 3의 제곱승 씩 개수 증가
// 3 나머지 연산 통해 자리수 카운트 (단, 나누어떨어질 경우 자리수 고려)
String answer = "";
int cn = n;
while(cn>0){
// 3 나머지 -> 4, 1, 2
if (cn % 3 == 0){
answer = "4" + answer;
cn--; // 나누어 떨어질 경우 자리수 바뀜
}else if(cn % 3 == 1){
answer = "1" + answer;
}else{
answer = "2" + answer;
}
cn /=3;
}
return answer;
}
}
'Archived(CSE Programming) > 알고리즘(Java)' 카테고리의 다른 글
| 프로그래머스 - 삼각 달팽이(Java, LV2) (0) | 2020.10.20 |
|---|---|
| 프로그래머스 - 스킬트리(Java, LV2) (0) | 2020.10.20 |
| 프로그래머스 - 경주로 건설(Java, LV3, 2020 카카오) (2) | 2020.10.19 |
| 프로그래머스 - 방문길이(Java, LV3) (0) | 2020.10.18 |
| 프로그래머스 - 숫자게임(Java, LV3) (0) | 2020.10.17 |

