https://programmers.co.kr/learn/courses/30/lessons/62048
코딩테스트 연습 - 멀쩡한 사각형
가로 길이가 Wcm, 세로 길이가 Hcm인 직사각형 종이가 있습니다. 종이에는 가로, 세로 방향과 평행하게 격자 형태로 선이 그어져 있으며, 모든 격자칸은 1cm x 1cm 크기입니다. 이 종이를 격자 선을 ��
programmers.co.kr
풀이
해당 문제는 사각형 패턴의 규칙을 찾는 것이 관건이었다.
(나는 3개의 예제를 그려보며 패턴이 있음을 파악했다... 수학적 사고가 뛰어난 사람들은 저게 1차함수를 활용하는 문제임을 알고 푼 듯하다)
먼저 대각선이 그어지는 패턴을 보면 어느 꼭짓점(좌표)에서 딱 맞게 떨어진다.
그림 출처 : ajufresh.log
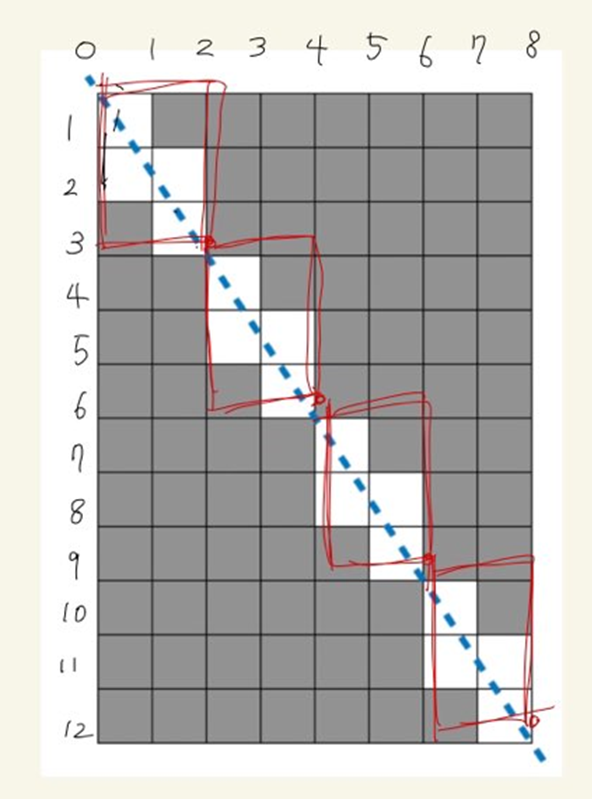
그렇기에, 딱 꼭짓점에 맞아 떨어지는 사각형 패턴을 가지고 와서 보면 된다.
즉, 저 빨간색 패턴만 두고 생각했을 때, 저 패턴 내에서 사용하지 못하는 사각형을 구하고 그 패턴이 몇개 나오는지를 계산하면 정답이 된다.
이 때, 패턴은 가로/최대공약수:세로/최대공약수 의 비율이 된다.
나는 이 비율을 wg, hg로 선언했다. 해당 패턴을 가지고 와서 보면 다음과 같다.
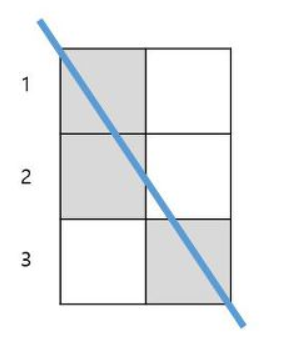
대각선은 가로만큼 가고, 세로만큼 가기에 wg+ hg 만큼 사용하지 못한다.
이 때, 가로와 세로가 겹치는 시작부분이 꼭 1개 존재한다(1,1).
즉 wg + hg -1 만큼 사용하지 못하는 것이다.
정답은 w * h -(wg + hg -1)의 공식이 완성한다. 단, long 형을 주의한다.
class Solution {
// 최소공약수 구하기
public int gcd(int a, int b){
int temp;
if (a>= b){
temp = a;
a = b;
b = temp;
}
while(b!=0){
temp = a % b;
a = b;
b = temp;
}
return a;
}
public long solution(int w, int h) {
long answer = (long)w* (long)h;
// 배수 구하기
long gcd_val = gcd(w,h);
long wg = w / gcd_val ;
long hg = h / gcd_val;
long diff = gcd_val * (wg + hg -1);
answer -= diff;
return answer;
}
}'Archived(CSE Programming) > 알고리즘(Java)' 카테고리의 다른 글
| 프로그래머스 - 섬 연결하기(Java, LV3) / MST (0) | 2020.10.17 |
|---|---|
| 프로그래머스 거스름돈(Java, LV3) /DP (0) | 2020.10.17 |
| 프로그래머스 - 주식가격(Java, LV2) (0) | 2020.10.16 |
| 프로그래머스 타겟 넘버 (2) | 2020.03.15 |
| 프로그래머스 큰 수 만들기 (0) | 2020.01.12 |
