문제
최소힙 만들기
힙이란 우선순위 큐라고도 불리며 말하는 것으로 다음과 같이
부모 노드의 값의 우선순위 자식 노드의 값의 우선순위보다 높은 상태를 말합니다.
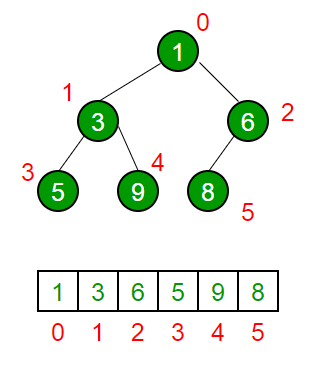
최소힙이란 값이 적은 것이 우선순위가 높은 것으로
Root Node에는 큐에서 가장 작은 값이 배정되어 있어야 합니다.
위의 우선순위 큐에서도 알 수 있듯이 1이 가장 작은 값이기에 Root Node가 됩니다.
해결 알고리즘
Heap도 일종의 Queue이기에 구현하는 데 있어 고려해야 할 것은 삽입(push)과 삭제(pop), 두 가지 입니다.
Push의 경우에는 Heap이라는 1차원 배열에다 값을 추가하는데 우선순위에 맞게 추가하면 됩니다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | // heap 삽입함수 void minHeap(int data, int * n) { // 끝 값 +1 int i = ++(*n); // 만약 MAX 넘으면 ERROR! if (i >= MAX) { fprintf(stderr, "HEAP FULL ERROR!\n"); exit(1); } // i 가 root가 아닐 동안 && 위치 찾지 못했을 동안 while (i != 1 && heap[i / 2] > data) { heap[i] = heap[i / 2]; // 부모 노드를 내리고 i = i / 2; //올라가기 } // 탈출하면 위치에 넣기 heap[i] = data; } | cs |
Pop의 경우에는 Root node(Index 1)의 값과 마지막 leaf Node의 값을 스왑해준 다음에
Heap의 개수를 한 개 줄이고,
위치를 재조정하는 방식으로 구현합니다.
이 때, 위치 재조정은 함수를 따로 구현해야 합니다.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 | // Pop 함수, size는 Heap의 data 개수 void heapPop(int size){ SWAP(heap[1], heap[size], temp); // 위치 바꾸고 size--; // 개수하나 뺴고 adjust(1, size); //위치 재조정 } // 위치 조정 void adjust(int parent, int n) { int child = parent * 2; // 자식 노드 int temp = heap[parent]; // 값 임시저장 // n을 벗어나지 않을 동안 while (child <= n) { // 둘 중 우선순위가 더 높은 자식 노드 값 if (heap[child] > heap[child + 1]) { child++; } // 벗어났으면 종료 if (child > n) { break; } // 자리 찾았으면 종료 if (heap[child] > temp) { break; } // 그렇지 않으면 내려가기 else { heap[child / 2] = heap[child]; child *= 2; } } // 위치에 넣기 heap[child / 2] = temp; } | cs |
'Archived(CSE Programming) > 자료구조(C++)' 카테고리의 다른 글
| 자료구조 프로그래밍 Lab06) 이항 힙 만들기 (Binomial Heap) (0) | 2018.11.03 |
|---|---|
| 자료구조 프로그래밍 Lab05) 최소 좌향 트리 만들기(Leftist Min Tree, Heap) (0) | 2018.11.03 |
| 자료구조 프로그래밍 Lab04) 그래프 모든 경로 찾기 C (두 vertex 사이) (0) | 2018.10.25 |
| 자료구조 프로그래밍_Lab02) 역대 최고가 주식 (0) | 2018.10.24 |
| 자료구조 프로그래밍_Lab01) 술 취한 바퀴벌레 문제 (0) | 2018.10.24 |

